서론
이 글에서는 시대팅 시즌5의 매칭 결과에 영향을 미친 주요 요인들을 분석한 내용을 다룬다. 특히 이번 학기 고급프로그래밍 강의에서 배운 로지스틱 회귀를 활용하여 분석을 진행하였는데, 이를 통해 매칭 알고리즘 개선을 위한 유용한 인사이트를 도출하고자 했다.
로지스틱 회귀 분석
기본 개념
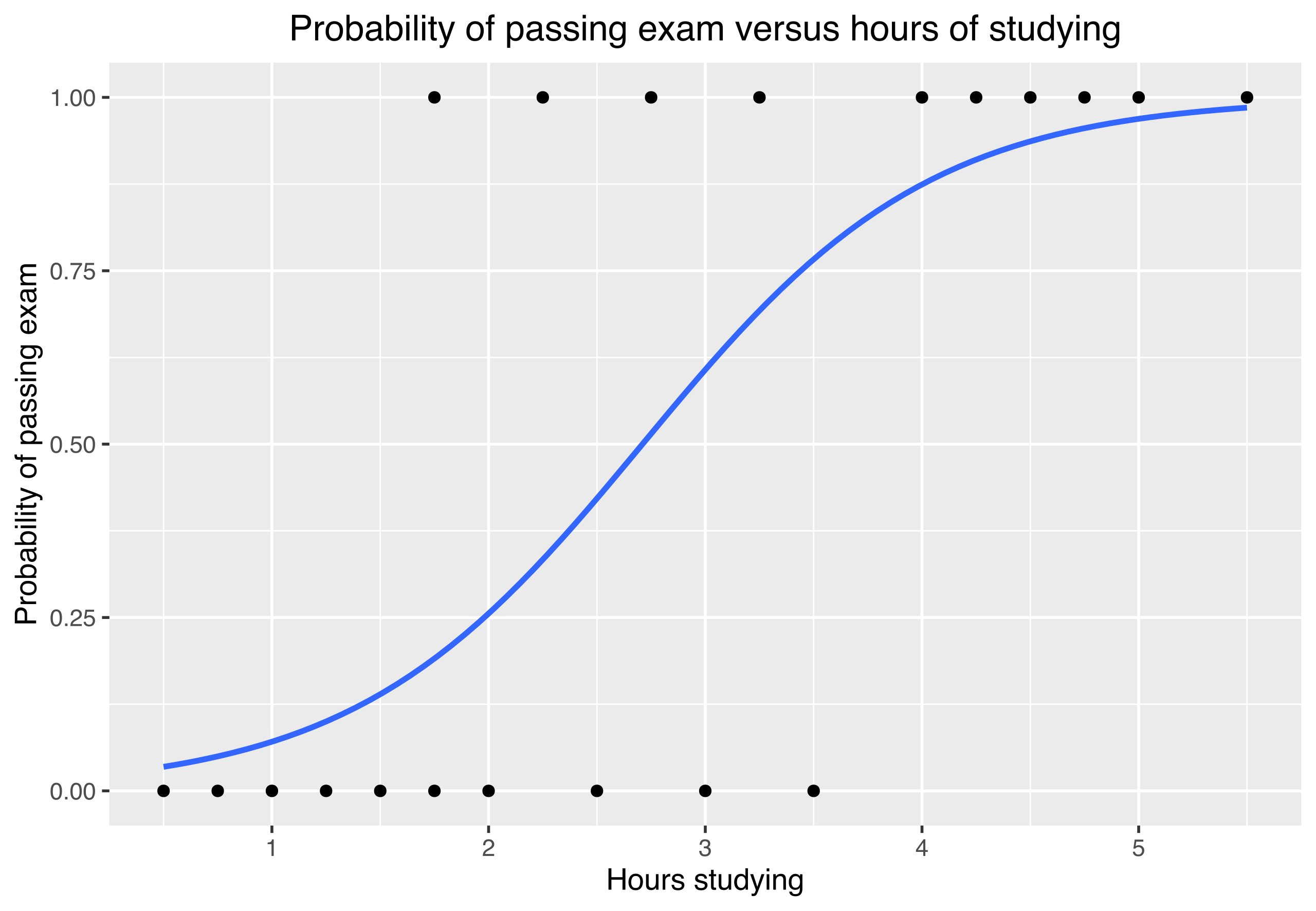학습 시간에 따른 시험 합격 확률을 나타낸 로지스틱 곡선
로지스틱 회귀(Logistic Regression)는 종속 변수가 이진 값(예: 예/아니오, 성공/실패)을 가질 때 사용하는 회귀 분석 기법이다. 이 기법은 선형 회귀를 기반으로 하면서, 결과를 확률로 해석할 수 있도록 시그모이드 함수를 사용한다.
시그모이드 함수는 다음과 같은 수식으로 정의된다.
\[S(x) = \frac{1}{1 + e^{-x}}\]여기서 $x$는 독립 변수와 가중치(weight)의 선형 결합인데, 일반적으로 다음과 같이 나타낼 수 있다.
\[x=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_nx_n\]- $\beta_0$: 절편(intercept) 값으로, 독립 변수가 0일 때의 초기값을 의미.
- $\beta_1, \beta_2, \cdots, \beta_n$: 각 독립 변수에 곱해지는 가중치(weight).
- $x_1, x_2, \cdots, x_n$: 독립 변수들.
이 함수의 출력값 $S(x)$는 $x$의 값에 따라 0과 1 사이의 연속적인 값이 되며, 이를 사건이 발생할 확률(probability)로 해석할 수 있다. 예를 들어, $S(x)$가 0.8이라면, 사건이 발생할 확률이 80%라는 의미로 이해할 수 있다.
선택 이유
이진 분류 예시
해당 분석 기법을 선택한 이유는 종속 변수(매칭 성공 여부)가 이진 분류(성공 또는 실패)였기 때문이다. 로지스틱 회귀는 선형 회귀와 유사하지만 출력값이 확률로 변환되기 때문에 이진 분류 문제에 적합하다. 또한, 변수 간의 관계를 명확하게 해석할 수 있어 매칭 성공률에 영향을 미치는 요인들을 파악하는 데 강점을 지닌다.
분석 데이터 소개
데이터 예시
| team_id | is_matched | age | height | prefer_age_min | prefer_age_max | prefer_height_min | prefer_height_max | prefer_appearance | prefer_eyelid | prefer_smoking | prefer_mbti |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | false | 23 | 176 | 21 | 30 | 150 | 190 | ARAB,NORMAL,TOFU | DOUBLE | FALSE | ESNFJP |
| 2 | true | 27 | 181 | 23 | 30 | 165 | 190 | NORMAL,TOFU | DOUBLE,INNER | FALSE | ISNFJP |
참고: 원본 데이터에 마스킹을 적용한 가명 데이터임.
분석에 사용한 데이터는 1대1 미팅을 신청한 남성 유저들의 정보이다(여성은 전원 매칭되어 제외). 이 데이터에서 매칭이 성공했는지 여부(is_matched)는 종송 변수로, 팀 ID(team_id), 나이(age), 키(height), 선호 설정 범위 점수(preference_range_score)는 독립 변수로 설정하였다.
선호 설정 범위 점수: 유저가 설정한 선호 항목들의 범위가 얼마나 넓은지를 나타내는 값이다. 이 점수는 유저가 각 항목(나이, 키, 얼굴상, 눈꺼풀, 흡연 여부, mbti)에 대해 설정한 선호 범위를 계산한 결과로, 범위를 넓게 설정할수록 더 높은 점수가 부여된다. 즉, 유저의 선호 항목 설정이 얼마나 유연하게 이루어졌는지를 나타낸다.
분석 과정
먼저, 데이터를 불러온 뒤 선호 설정 범위 점수를 계산하였다. 이후 확인하고자 하는 변수를 선택하고 데이터를 훈련용과 테스트용으로 나누었다. 마지막으로 statsmodels의 Logit 함수를 사용하여 로지스틱 회귀 모델을 학습시키고 그 결과를 출력했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
import pandas as pd
import statsmodels.api as sm
from sklearn.model_selection import train_test_split
# 데이터 로드
df = pd.read_csv('./data/single_male.csv')
APPEARANCE_TYPE = ["ARAB", "NORMAL", "TOFU"]
EYELID_TYPE = ["DOUBLE", "SINGLE", "INNER"]
SMOKING_TYPE = ["CIGARETTE", "E_CIGARETTE", "FALSE"]
# 선호 비율 계산
def calculate_age_ratio(prefer_age_min, prefer_age_max):
return (prefer_age_max - prefer_age_min + 1) / 11 # 20~30세
def calculate_height_ratio(prefer_height_min, prefer_height_max):
return (prefer_height_max - prefer_height_min + 1) / 41 # 150~190cm
def calculate_mbti_ratio(prefer_mbti):
return len(prefer_mbti) / 8
def calculate_preference_ratio(preference_column, options):
selected_preferences = preference_column.split(",")
return len(selected_preferences) / len(options)
df['appearance_ratio'] = df['prefer_appearance'].apply(lambda x: calculate_preference_ratio(x, APPEARANCE_TYPE))
df['eyelid_ratio'] = df['prefer_eyelid'].apply(lambda x: calculate_preference_ratio(x, EYELID_TYPE))
df['smoking_ratio'] = df['prefer_smoking'].apply(lambda x: calculate_preference_ratio(x, SMOKING_TYPE))
df['age_ratio'] = df.apply(lambda x: calculate_age_ratio(x['prefer_age_min'], x['prefer_age_max']), axis=1)
df['height_ratio'] = df.apply(lambda x: calculate_height_ratio(x['prefer_height_min'], x['prefer_height_max']), axis=1)
df['mbti_ratio'] = df['prefer_mbti'].apply(calculate_mbti_ratio)
# 선호 설정 범위 점수 계산
df['preference_range_score'] = (
df['appearance_ratio'] *
df['eyelid_ratio'] *
df['smoking_ratio'] *
df['age_ratio'] *
df['height_ratio'] *
df['mbti_ratio']
)
# 주요 변수 선택
features = ['team_id', 'age', 'height', 'preference_range_score']
target = 'is_matched'
X = df[features]
y = df[target]
# 훈련, 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 상수항 추가
X_train_transformed = sm.add_constant(X_train)
X_test_transformed = sm.add_constant(X_test)
# 모델 학습
logit_model = sm.Logit(y_train, X_train_transformed)
result = logit_model.fit()
# 결과 출력
print(result.summary())
분석 결과
로지스틱 회귀 모델을 사용하여 매칭 성공률에 영향을 미치는 요인들을 분석한 결과는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Optimization terminated successfully.
Current function value: 0.317971
Iterations 8
Logit Regression Results
==============================================================================
Dep. Variable: is_matched No. Observations: 432
Model: Logit Df Residuals: 427
Method: MLE Df Model: 4
Date: Mon, 09 Dec 2024 Pseudo R-squ.: 0.4992
Time: 14:57:24 Log-Likelihood: -137.36
converged: True LL-Null: -274.28
Covariance Type: nonrobust LLR p-value: 4.780e-58
==========================================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------------
const -55.6472 7.975 -6.977 0.000 -71.279 -40.016
team_id 0.0090 0.001 9.983 0.000 0.007 0.011
age 0.0493 0.064 0.768 0.443 -0.077 0.175
height 0.2602 0.041 6.401 0.000 0.181 0.340
preference_range_score -0.5935 0.741 -0.801 0.423 -2.046 0.859
==========================================================================================
주요 변수 해석
- 팀 ID (
team_id): 팀 ID는 매칭 성공률에 중요한 영향을 미쳤다. 회귀 계수(coef)는 0.009로, 팀 ID가 증가할수록 매칭 성공 확률이 증가한다는 것을 의미한다. p-value는 0.000으로 매우 유의미한 변수로 확인되었다. - 나이 (
age): 나이는 매칭 성공률에 유의미한 영향을 미치지 않았다. 회귀 계수(coef)는 0.0.0493로 미미한 영향을 주지만, p-value가 0.443로 통계적으로 유의미하지 않았다. - 키 (
height): 키는 매칭 성공률에 중요한 영향을 미쳤다. 회귀 계수(coef)는 0.2602로, 키가 증가할수록 매칭 성공 확률이 높아진다는 것을 의미한다. p-value는 0.000으로 매우 유의미한 변수이다. - 선호 설정 범위 점수(
preference_range_score): 선호 설정 범위 점수는 매칭 성공률에 부정적인 영향을 미쳤다. 회귀 계수(coef)는 -0.5935로, 점수가 높을수록 매칭 성공 확률이 낮아지는 경향이 있었다. 그러나 p-value가 0.423으로 유의미하지 않은 변수로 확인되었다.
결과 해석
로지스틱 회귀 분석을 통해, 팀 ID와 키가 매칭 성공률에 중요한 영향을 미친다는 결과를 얻을 수 있었다. 특히 팀 ID는 매칭 성공률과의 상관관계가 강하게 나타났는데, 이는 신청 시점이 성공률에 영향을 미쳤음을 시사한다. 키 또한 중요한 변수로, 키가 높은 사람일수록 매칭 성공 확률이 높아진다는 결과가 나왔다. 이는 여성 참가자들이 키를 핵심 선호 항목으로 선택한 경향성 때문인 것으로 보인다. 반면, 나이와 선호 설정 범위 점수는 매칭 성공률에 유의미한 영향을 미치지 않았다.
매칭 성공률 시각화
로지스틱 회귀 분석 결과 유의미한 변수로 밝혀진 팀 ID(team_id)와 키(height)에 대해 시각화를 진행하였다.
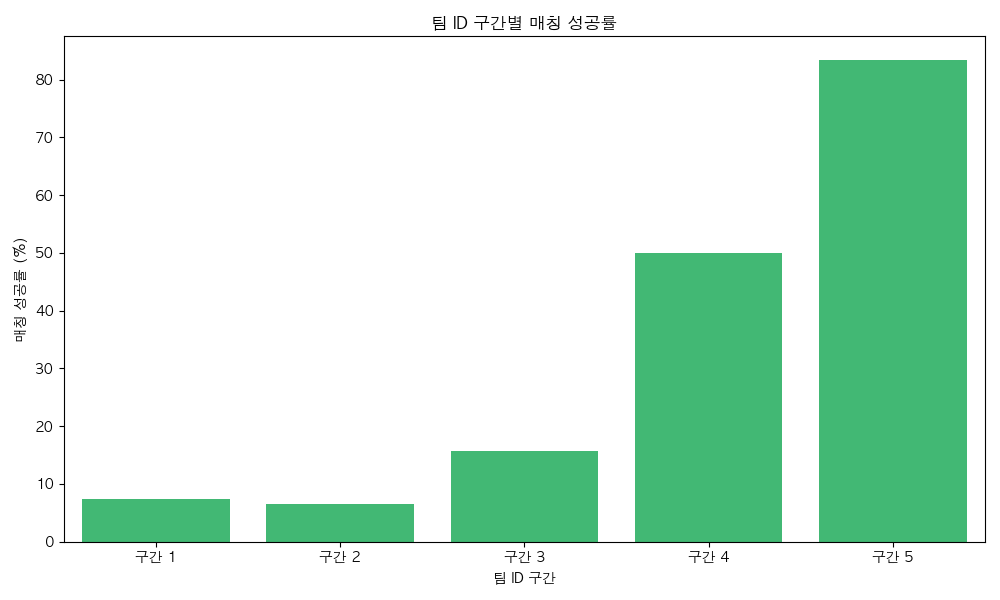
팀 ID
팀 ID를 구간별로 살펴본 결과, 뒤로 갈수록 매칭 성공률이 가파르게 상승한다는 특징을 발견했다. 즉, 신청기간 후반부에 신청한 유저들의 성공률이 초반부에 비해 월등히 높았다.
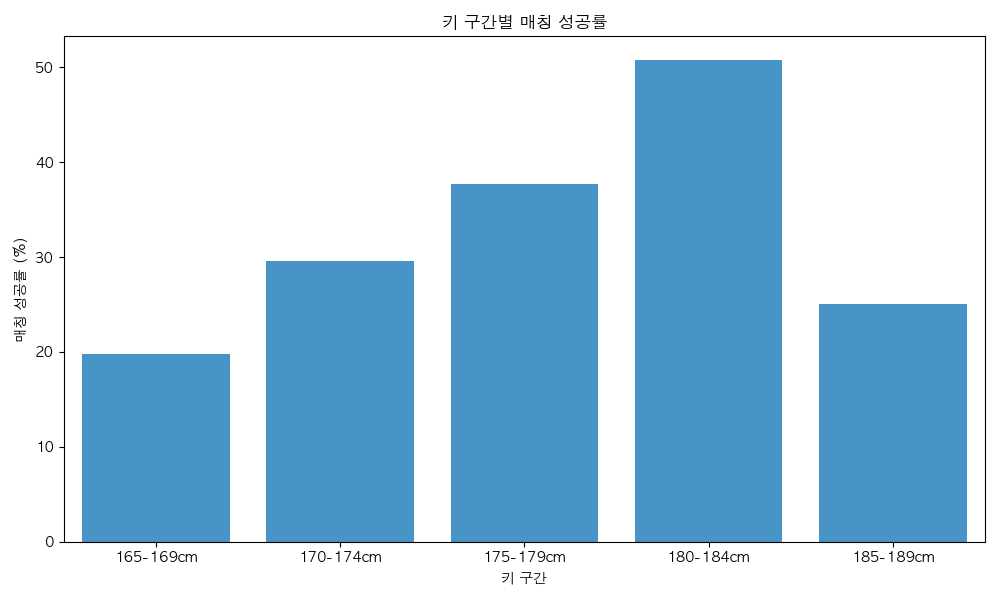
키
키에 따른 성공률을 살펴본 결과, 180cm 근방의 유저들의 성공률이 높게 나타났다. 특히 180~184cm 구간에서 매칭 성공률이 가장 높았다.
결론
이번 로지스틱 회귀 분석은 매칭 성공률에 영향을 미치는 주요 변수들을 확인하고, 이를 기반으로 매칭 알고리즘의 성능 개선 방향을 탐색하는 데 의의가 있었다. 특히 팀 ID와 키는 매칭 성공률과의 상관관계가 뚜렷했으며, 이를 통해 신청 시점과 키를 고려한 매칭 정책 설정의 필요성을 느꼈다.
분석을 통해 이번 매칭 알고리즘의 문제를 알 수 있었다. 매칭 성공 유저가 신청기간 후반부에 편중된 현상이었는데, 이는 Hospital-Resident 알고리즘의 입력 데이터 순서 의존성과 관련있는 것으로 보인다. 이러한 문제는 매칭의 공정성 측면에서 개선의 여지가 있다.
이번 분석은 최근 배운 통계 기법인 로지스틱 회귀를 실제 데이터에 적용해보는 소중한 기회였다. 이를 통해 데이터 기반 의사결정의 중요성을 실감했고, 분석 결과를 앞으로의 서비스 개선 방향에 반영할 수 있었다.