방법 구상
char *형태의 인자를int형으로 변경- 자료형에 저장
- 중복 체크
- 정렬 여부 체크
- 명령어 구현
- 알고리즘 구현
자료 구조
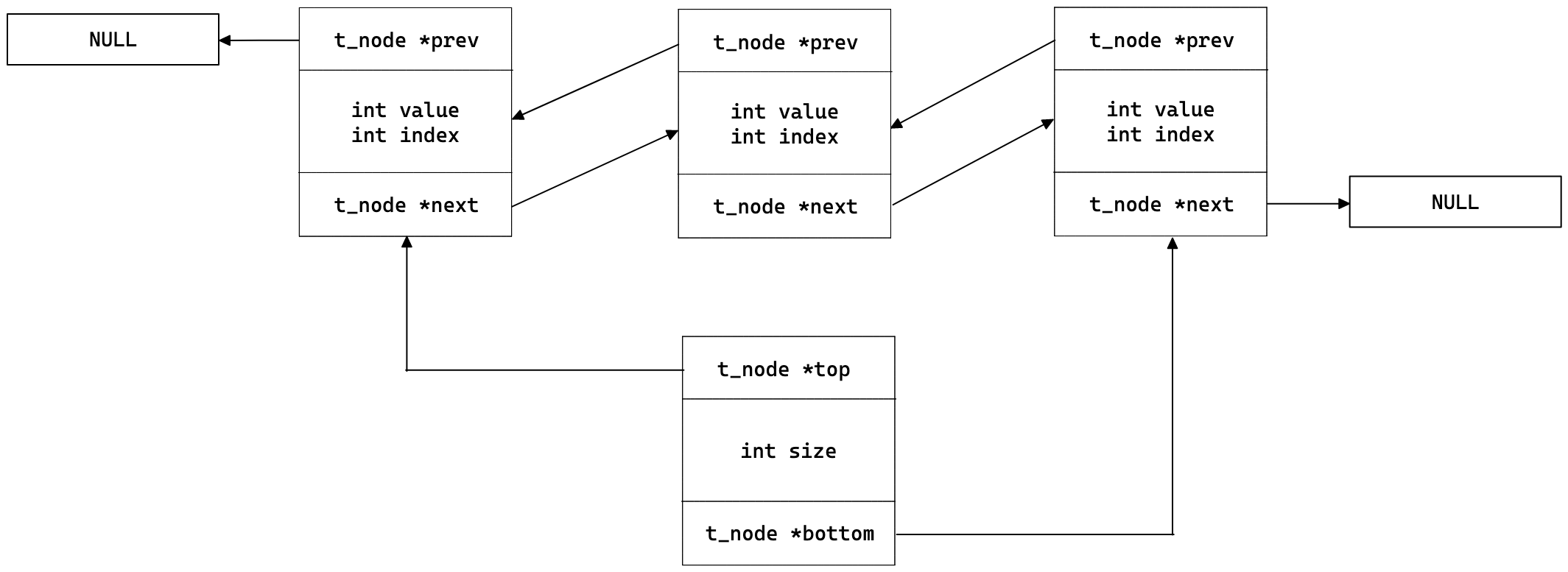
이중 연결 리스트 (Doubly Linked List)
인자를 저장할 자료형으로 각 node들이 서로 연결되어있는 이중 연결 리스트를 사용했다. 여기에 시작과 끝 node의 주소는 stack의 top, bottom에 저장되는 구조로 스택을 구현했다.
1
2
3
4
5
6
7
typedef struct s_node
{
int value;
int index;
t_node *prev;
t_node *next;
} t_node;
1
2
3
4
5
6
typedef struct s_stack
{
int size;
t_node *top;
t_node *bottom;
} t_stack;
우선 연결 리스트를 선택한 이유는 명령어를 적용할 때마다 수의 이동이 필요한데, 배열과 비교했을 때 요소를 삽입/삭제하는 과정이 더 쉽기 때문이다. 배열의 경우 새로운 공간에 모든 요소를 다시 저장해야 하지만 연결리스트는 해당 노드의 연결만 수정하면 된다.
또한 Libft에서 구현했었던 단일 연결 리스트(singly linked list)가 아닌 이중 연결 리스트를 사용한 이유는 정렬하는 과정에서 노드를 next 방향 외에 previous 방향으로도 탐색할 수 있도록 하기 위함이었는데… 결과적으로는 prev 멤버는 정렬하는데에 사용되지 않아서 굳이 이중 연결 리스트로 구현할 필요는 없었던 같다.
인자의 처리
작동 과정
- 따옴표로 묶은 인자는 하나의 인자로 처리되는 문제→split을 사용해 인자를 분리
- 분리한 인자를 atoi로 변환한 후 연결 리스트에 저장
- 들어온 수 간의 중복이 없는지 체크
- 각 수의 대소를 비교해 상대적인 수(인덱스)를 부여(ex. {7,4,2,10} → {2,1,0,3})
- 정렬된 상태인지 체크
과제에서 평가하는 기준이 알고리즘의 시간복잡도나 작동 시간이 아닌, 출력된 명령어의 개수이기 때문에 정렬하기 전 최대한 값을 정리해주기 위해 인덱스를 부여해 주었다. 간혹 인자로 간격이 큰 값들이 들어올 수 있는데(ex. -1000000, 1, 2, 3, 4, 5, 6), 이 경우 뒤에 정렬을 하기 위해 피봇을 고르는 과정에서 이상적인 피봇(수를 정확히 2:1:1로 나누는 두 값)이 아닌 값이 피봇(-499997, -749998)이 된다. 인덱싱은 이를 방지하기 위함이다.
명령어 처리 방법
연결리스트를 새로 이어주는 과정을 거친다.
- 위치가 바뀐 node는 다시 이어줌
- stack의 top, bottom에 node의 처음과 끝 주소를 다시 저장함
정렬 알고리즘
알고리즘의 종류
- 모래시계
- 그리디 알고리즘
- 병합 정렬
- 퀵 정렬 …
본과정에서 push swap 평가를 5번 정도 하였는데 그 때마다 모래시계 정렬, 그리디 알고리즘, 병합 정렬 등 다양한 방식을 접했었다. 그 중 모래시계 방식이 코드는 제일 간단하게 구현할 수 있을 것 같았지만 직관적이지가 않았고 그리디 알고리즘은 이해하는 것은 제일 쉬웠지만 구현하기엔 어려워보였다. 따라서 다른 방법을 찾아서 사용하게 되었다.
정렬 원리
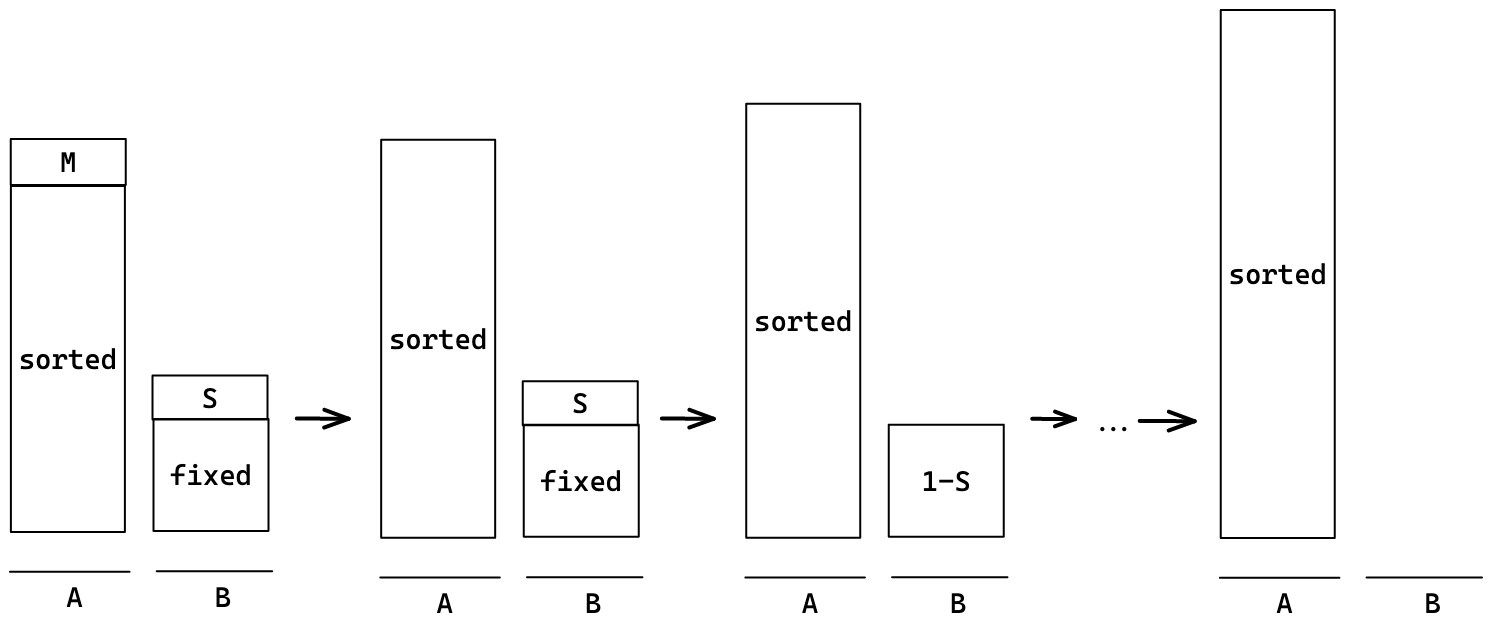
정렬의 핵심 원리는 세 덩어리로 나눈 뒤에 큰 덩어리부터 차례대로 정렬해 나가는 것이다.
처음의 제일 큰 덩어리를 다시 쪼개어 세 덩어리로 나누고, 그 중 큰 덩어리를 다시 세 덩어리로 나누는 과정을 특정한 개수가 될 때까지 반복한다. 그렇게 큰 덩어리의 정렬을 마친 뒤에 중간 덩어리(위의 과정을 반복함)를 정렬하고 마지막으로 작은 덩어리를 정렬하고 끝낸다.
피봇의 선택
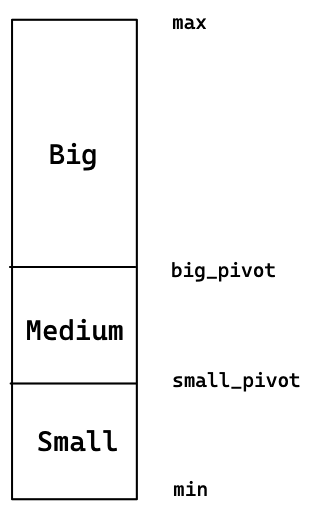
피봇은 다음과 같이 max, min의 평균을 큰 피봇으로, 큰 피봇과 min의 평균을 작은 피봇으로 설정하였다.
이를 통해 세 개의 덩어리(Big, Medium, Small)로 나눌 수 있게 된다.
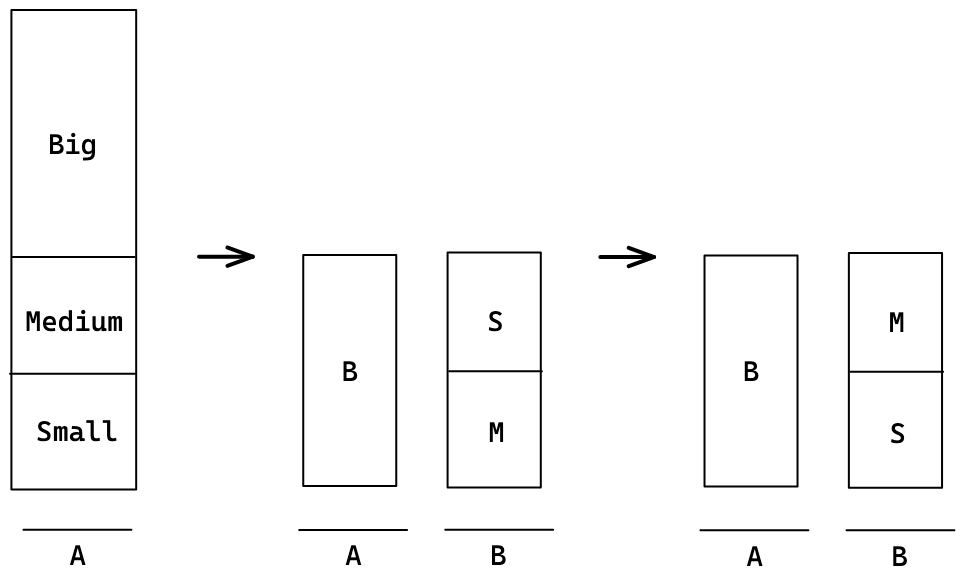
정렬 과정
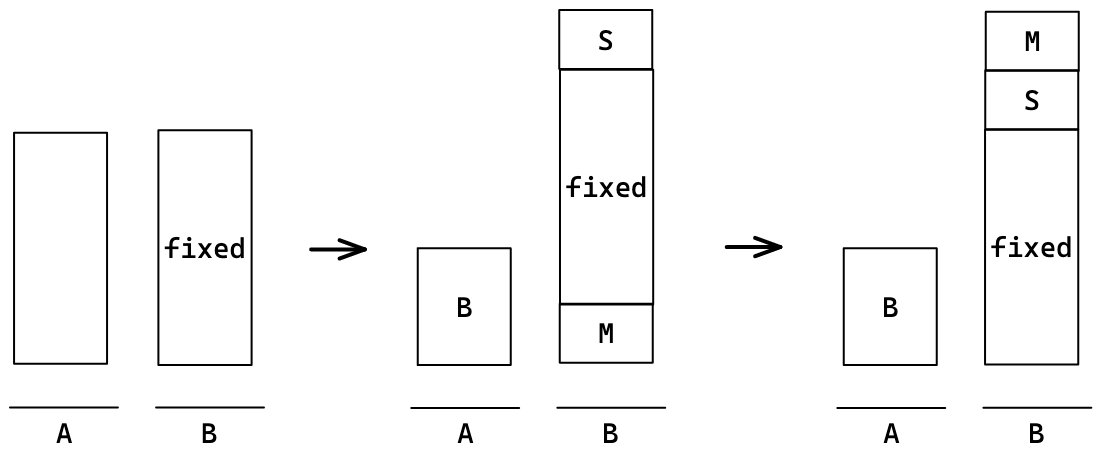
우선 B를 제외하고는 pb를 사용해 스택 B로 넘긴다. 넘길 때 M과 S를 구분해 두기 위해 M의 경우 rb를 한다. 넘기는 과정이 끝나면 rrb를 통해 M을 제일 위로 올려준다.(고정하기 전에 형태를 맞춰두기 위해)
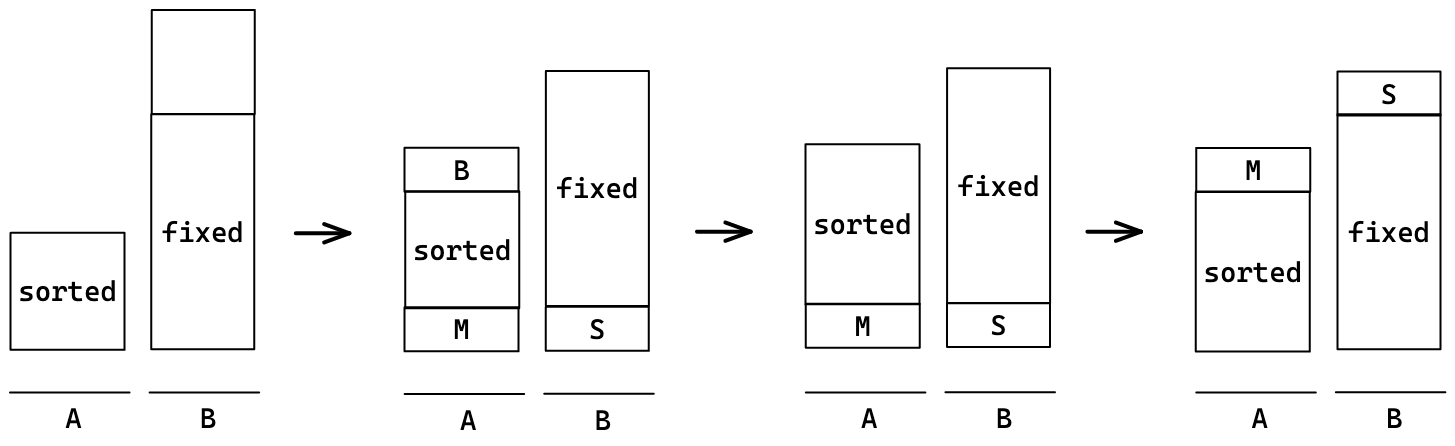
이전에 대강 정리해둔 스택 B의 M과 S는 고정시켜두고 B부터 다시 정렬한다.(이때는 재귀함수를 이용하였다.) 기존의 B를 다시 세 개의 덩어리로 나누어 B를 제외하고는 스택 B로 넘긴다. 이 과정을 B의 크기가 3개 이하가 될 때까지 반복한다. 3개 이하가 되면 직접 대소비교해서 정렬한다.
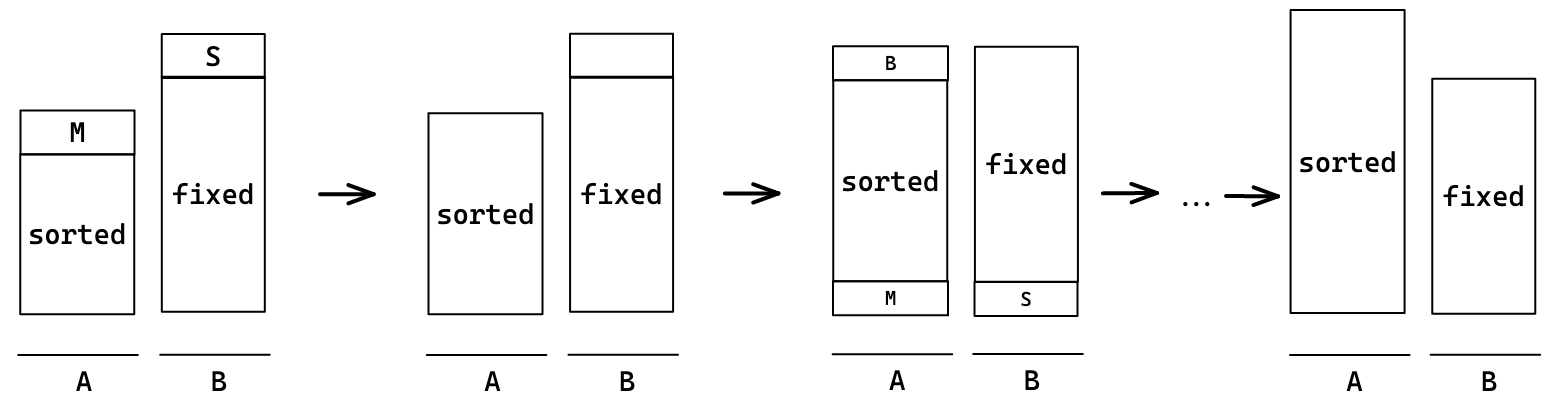
결과적으로 A에는 정렬된 수만 남았다. 이제부터는 직전의 M을 정렬해나간다. 이전과 같이 세 덩이로 나누어 이것의 B부터 정렬한다. 이때는 스택 A에도 아래에 M이 있기 때문에 둘 다 다시 위로 올려준다.
M이 3개 이하가 되면 직접 정렬한다.(아니면 위 과정 반복) 이전의 S를 다시 세 덩어리로 나누어 정렬을 반복한다. 결과적으로 맨 처음의 M, S를 제외하고 모두 스택 A에 정렬이 되었다.
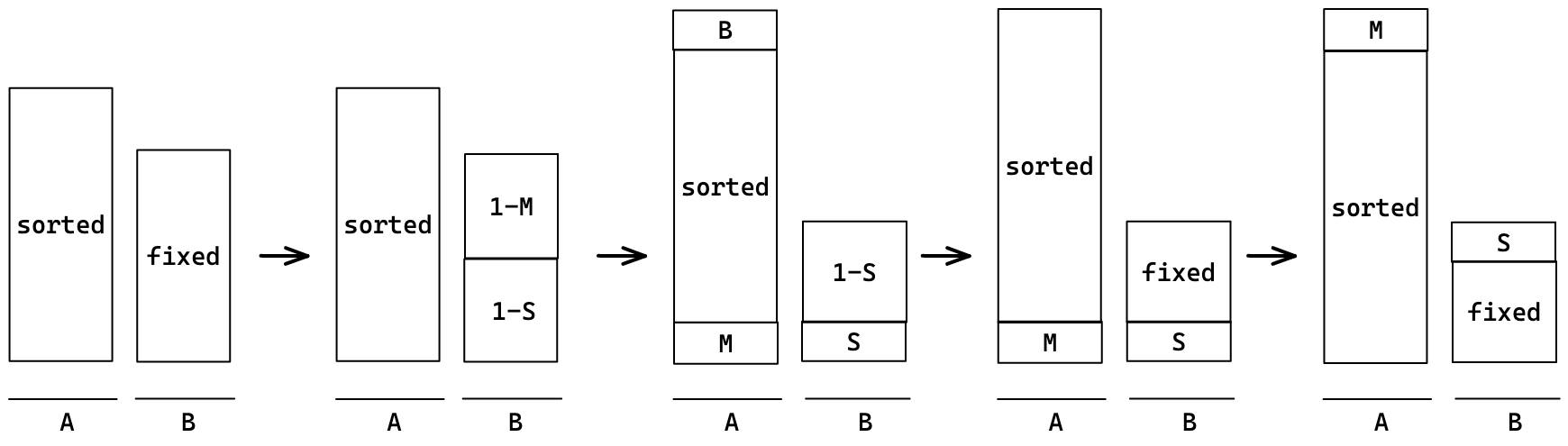
1-M(맨 처음의 중간 덩어리)을 정렬한다.
이 과정을 반복해서 1-S까지 정렬하면 스택 A에 모든 수가 정렬된다.
적은 수의 정렬
적은 수를 처리하는 경우 직접 대소비교를 해 하드 코딩해주었다.
하드 코딩을 사용하는 곳이 두 곳이 있는데, 맨 처음 인자를 받아 처리하는 부분과 정렬할 때 최소 크기를 처리하는 부분이다.
인자가 5개 이하인 경우
- 인자 2개
순서가 반대일 것(정렬되었다면 main문에서 이미 처리되었음)이기 때문에 sa해줌.
- 인자 3개 이상
스택 A에 큰 숫자 3개만 남기고 나머지는 B로 옮김
max를 기준으로 구분해서 정렬함
B에 있는 남은 수를 정렬해서 A로 돌려보냄
정렬의 최소 크기
정렬을 계속하다가 한 덩어리에 포함된 수가 3개 이하가 되면 직접 정렬해주었다.
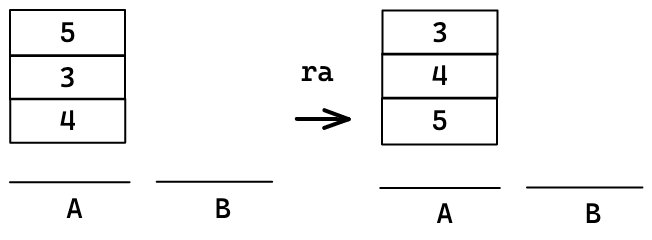
이 부분은 초반에 인자를 정렬하는 방식과는 조금 다르게 하였다. 인자를 처리할 때는 sorted되거나 fixed된 부분이 없이 인자로만 이루어졌기 때문에 ra를 통해 덩어리의 제일 위 값을 덩어리의 제일 아래로 옮길 수 있었다.
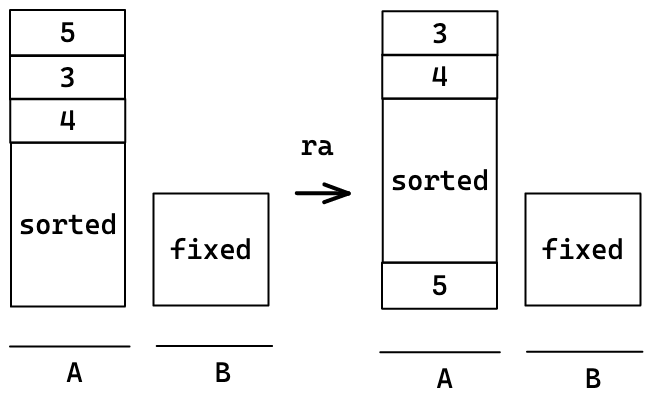
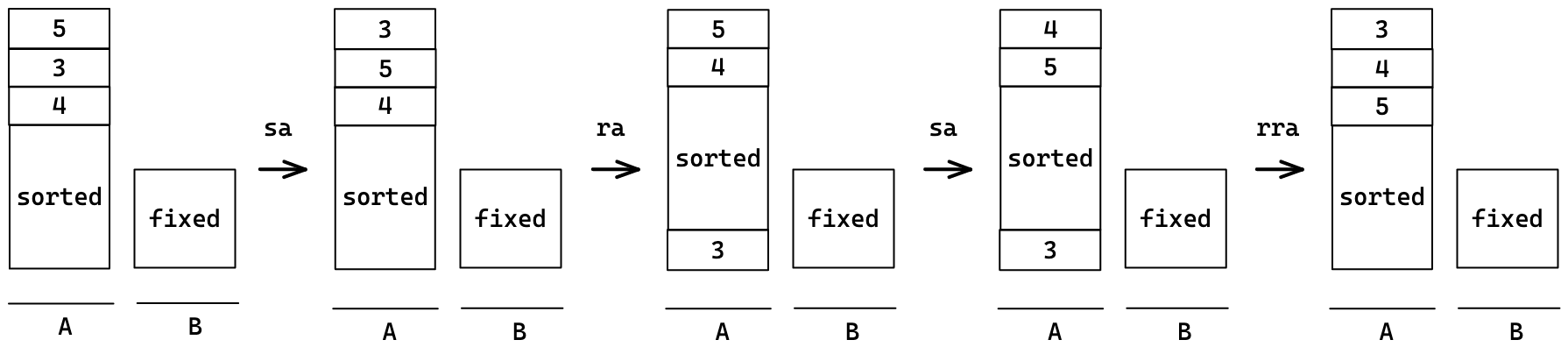
하지만 정렬하는 과정에서는 이 방법을 사용할 수 없게된다.
따라서 아래와 같이 sorted와 fixed를 건드리지 않고 정렬해야 한다.
Checker 구현
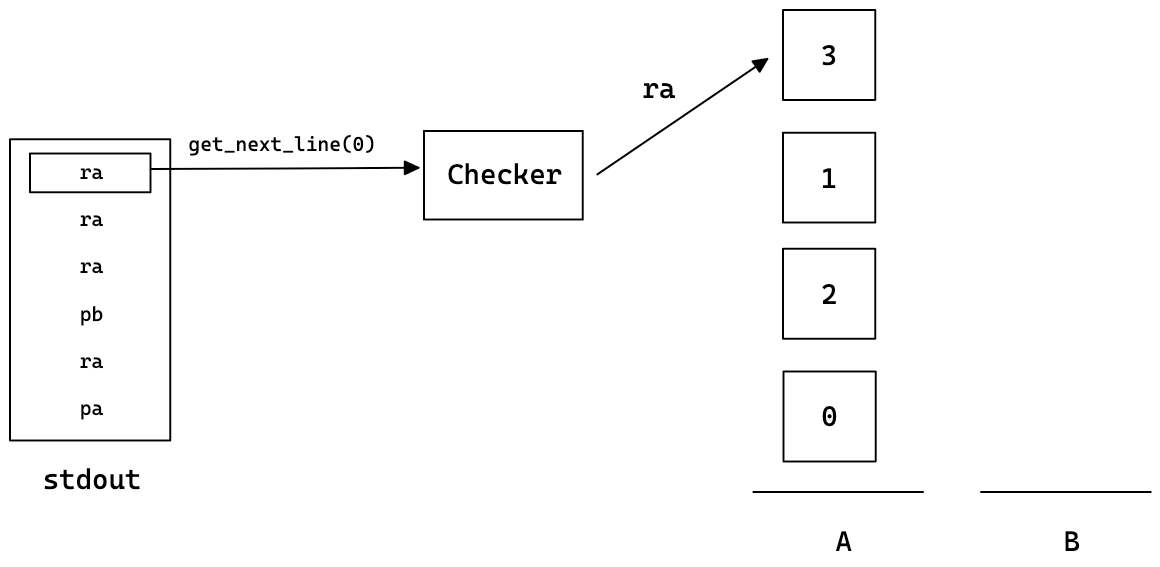
보너스 파트의 체커는 표준입력으로 들어온 명령어가 인자의 정수들을 제대로 정렬하는지를 판단하는 프로그램이다.
기본적으로 인자 파싱과 에러 출력은 필수 파트와 동일하게 이루어진다.
여기서는 이전에 구현한 get_next_line을 사용하여 표준 입력을 받아오게 하였다.
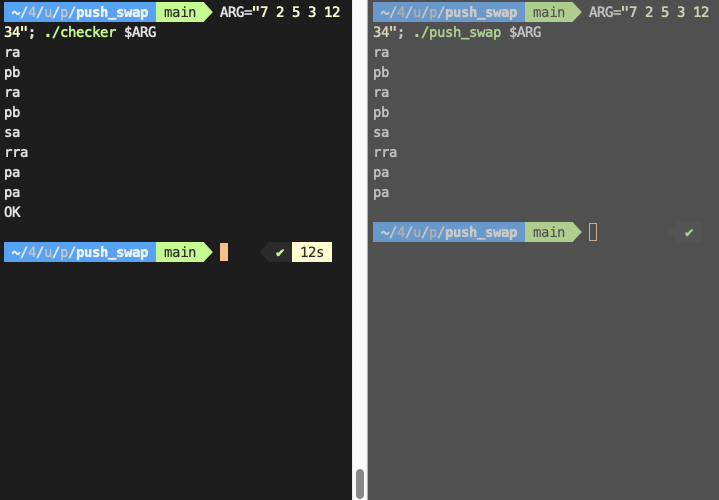
표준 입력으로 들어온 명령어를 받아오는 방식이기 때문에 위와 같이 파이프를 통해 push_swap의 명령어 결과를 바로 넘겨받는 것 뿐만 아니라
이처럼 터미널 상에서 ctrl+D로 EOF를 입력할 때까지 입력된 명령어를 받아오는 것도 가능하다.
테스트
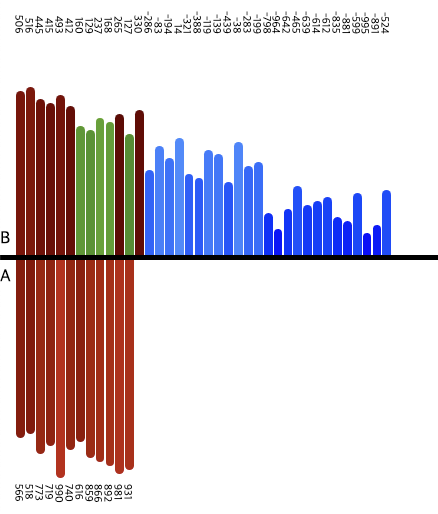
작동 과정
- 인자 50개
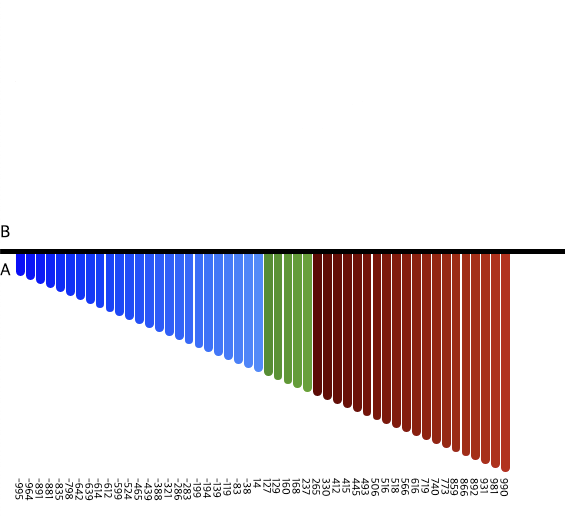
- 인자 100개
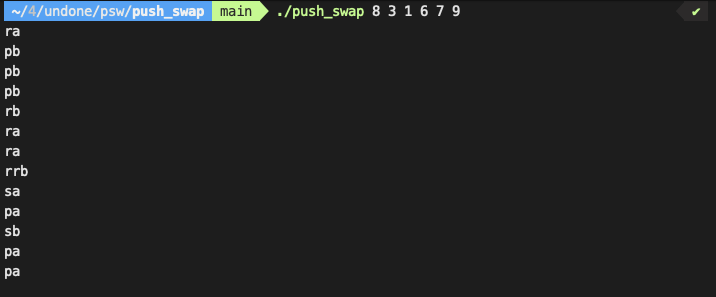
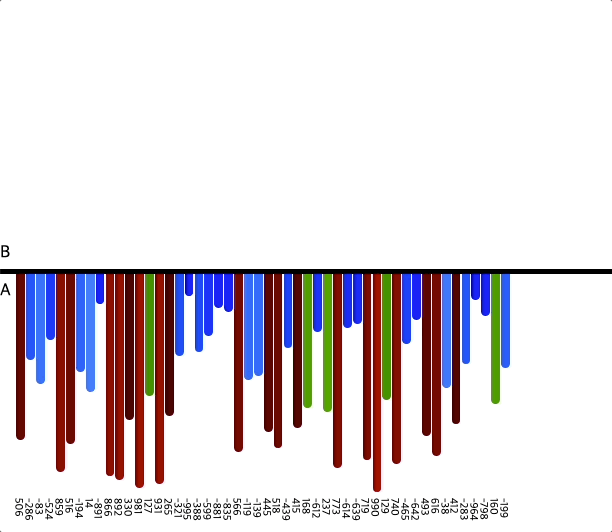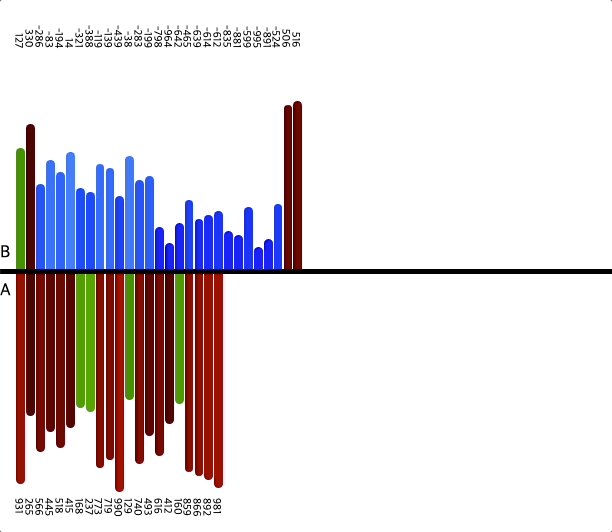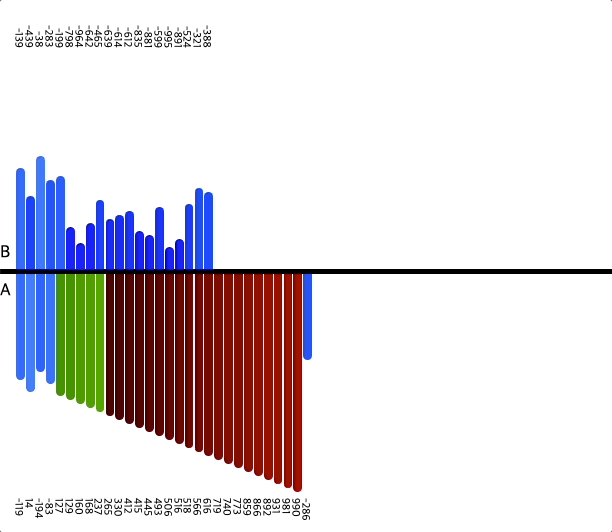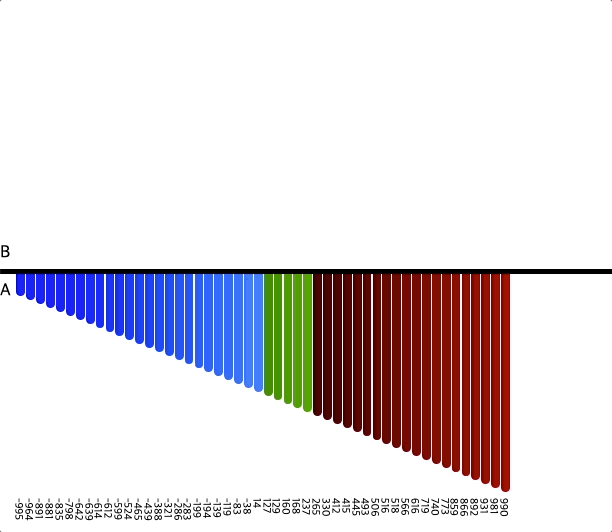
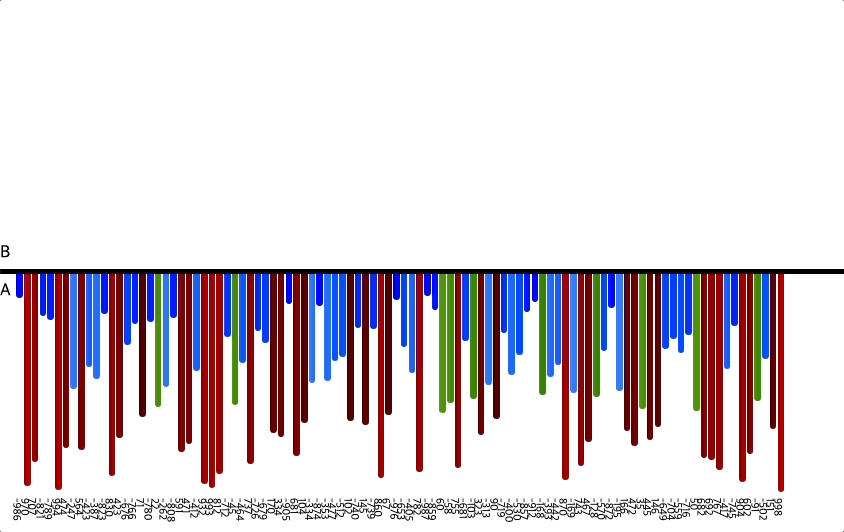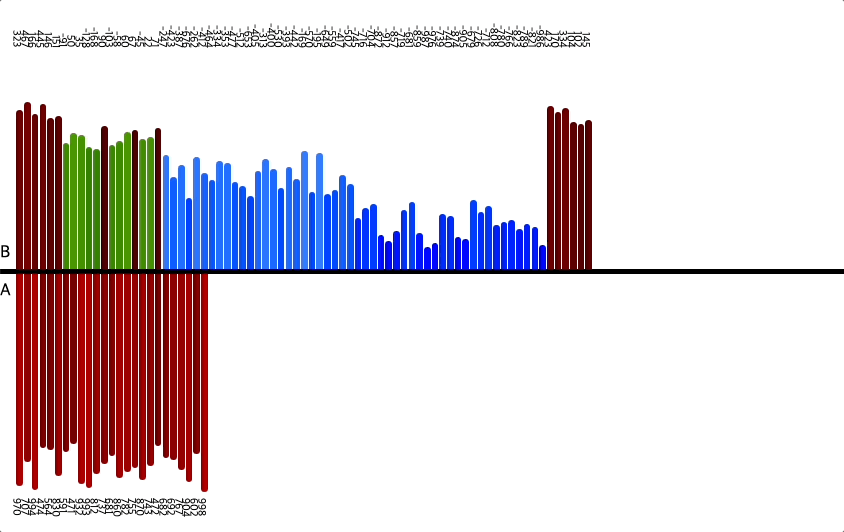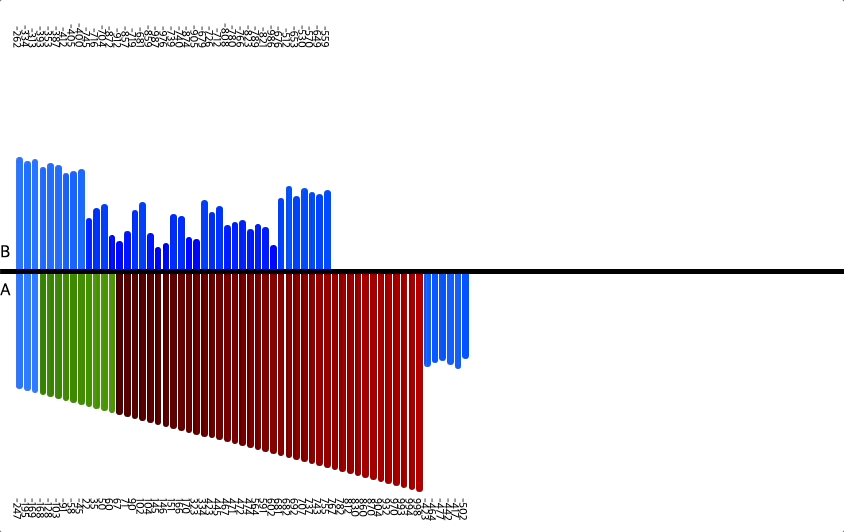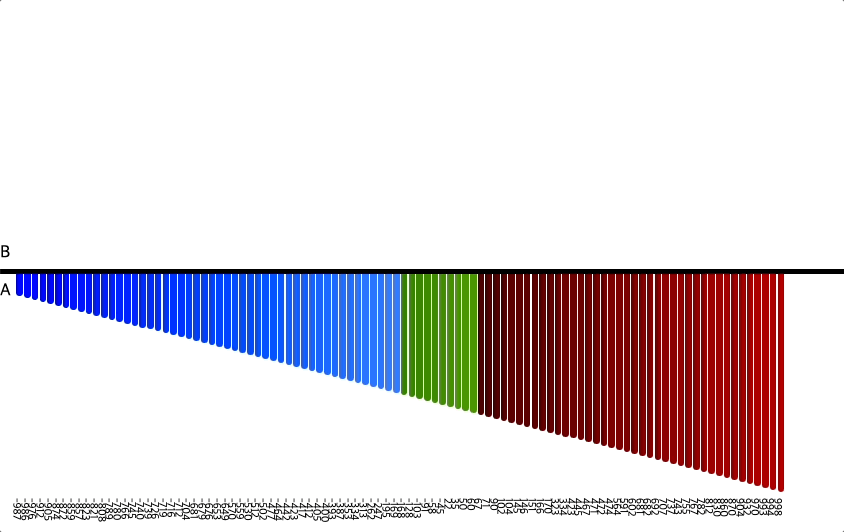
위 이미지를 통해 정렬하는 과정을 확인할 수 있다.
위에서 설명한 것과 같이 세 덩어리로 나누고, 차례차례 정렬해서
모든 수를 정렬하는 것을 볼 수 있다.
성능 테스트
기준
- 인자 3개 : 3회
- 인자 5개 : 12회
- 인자 100개 : 700 / 900 / 1100 / 1300 / 1500 (각각 5 ~ 1 점)
- 인자 500개 : 5500 / 7000 / 8500 / 10000 / 11500 (각각 5 ~ 1 점)
방법
랜덤 숫자 생성
터미널 상에서
ruby -e "puts (1..500).to_a.shuffle.join(' ')"
시각화 도구
온라인
- 프로그램 1 https://github.com/hermin9804/push_swap_visualizer
- 프로그램 2 https://github.com/o-reo/push_swap_visualizer
테스터
테스트 결과
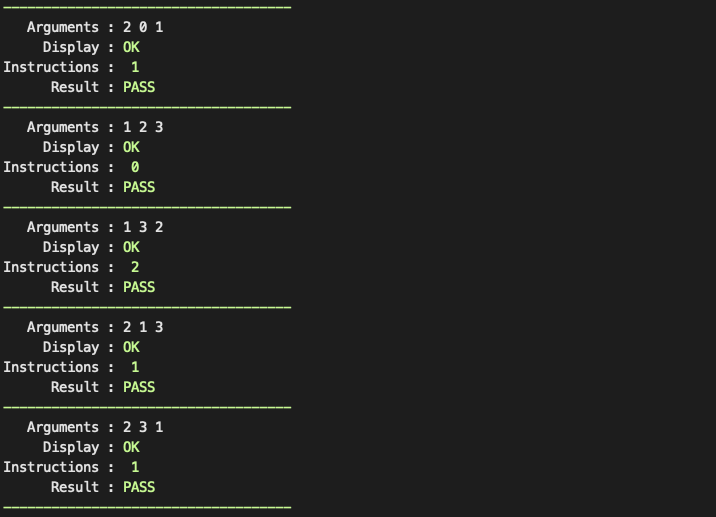
인자가 3개일 때 명령어가 0~2개 나왔다
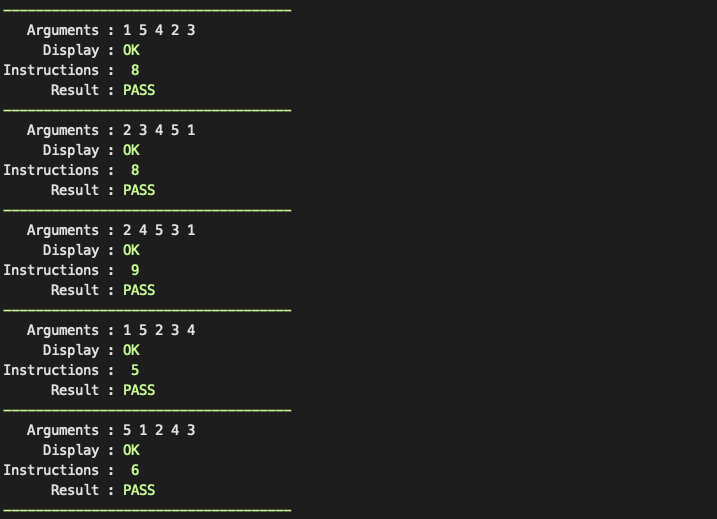
인자가 5개일 때는 5~9개 나왔다
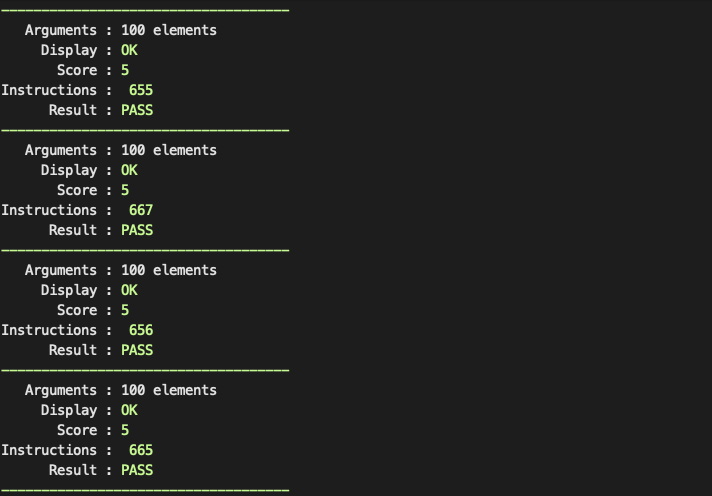
100개일 때는 대략 660개 정도 나왔다
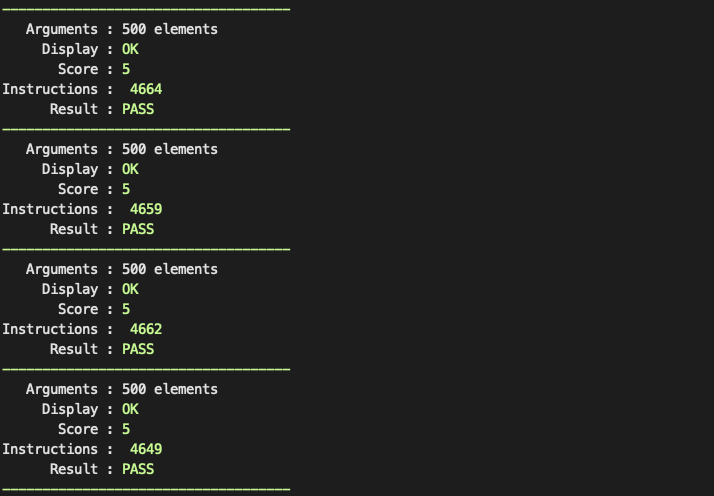
500개일 때는 4660개 정도 나왔다
총평
다양한 예외처리를 한 덕분에 평가에서의 큰 문제는 없었다. 하지만 보너스 파트에서 주어진 checker_Mac과 내가 만든 checker가 다르게 동작하는 부분이 있었다.
개선 방향
- 알고리즘에 대해 직접 고민하는 시간이 부족했던 것 같음
- checker가 checker_Mac과 다르게 동작하는 부분
- 보너스의 atoi를 변형해서 처리해줌
- 과제의 common instruction과 부합하지 않은 컴파일러의 사용